Summary of Contributions
Data-perspective understanding. We understand the generalization benefit of model invariance via characterizing the sample-dependent properties of data transformations. We introduce the notion of sample cover induced by data transformations and establish connections between the small sample covering number of data transformations and the small generalization bound of invariant models. Since this general connection requires a strong assumption on data transformations to be instructive, we relax the assumption by further assuming the Lipschitzness of model class to get a refined generalization bound. To understand the generalization benefit of model invariance in a more interpretable way, we also consider linear model class and show that the model complexity of invariant models can be much smaller than its counterpart, depending on the sample-dependent properties of data transformations.
Guidance for data transformation selection. To guide the data transformation selection in practice, we propose to use the sample covering number induced by data transformations as a suitability measurement to estimate the generalization benefit for invariant models.This measurement is model-agnostic and applies generally to any data transformation.We also introduce an algorithm to estimate the sample covering number in practice.
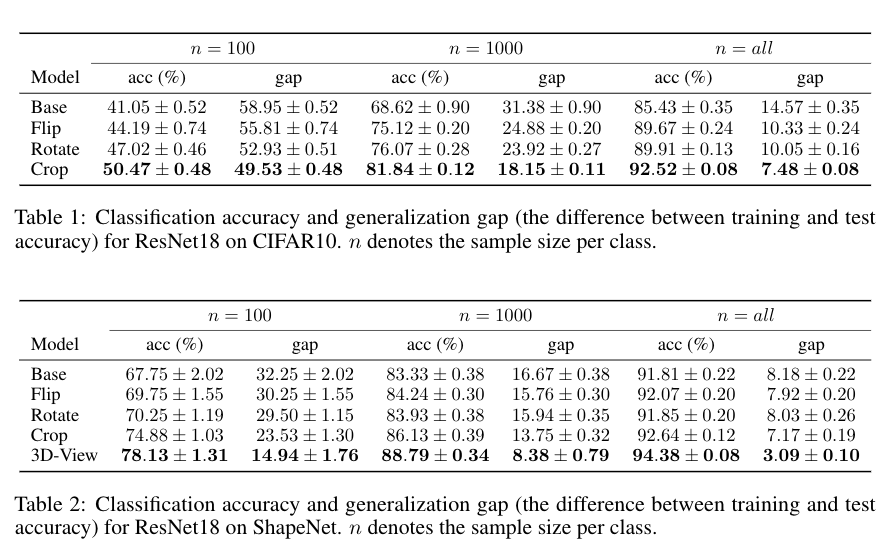
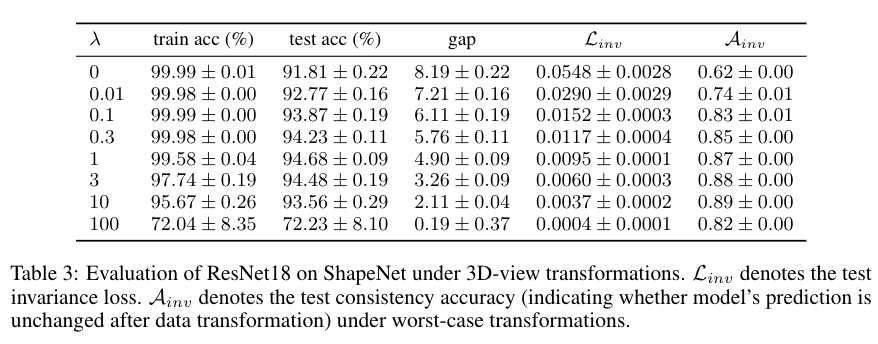
Empirical evaluations. We empirically estimate the sample covering number for some common data transformations on CIFAR-10 and ShapeNet (a 3D-dataset) to evaluate their potential generalization benefit. The 3D-view transformation renders smaller empirical sample covering number than others by a large margin on ShapeNet, while cropping is the most favorable among others. Then, we do invariant model training under those data transformations by data-augmentation and invariance loss penalization to evaluate the actual generalization benefit for invariant models. Results show clear correlation between smaller sample covering numbers of data transformations and better generalization benefit for invariant models.