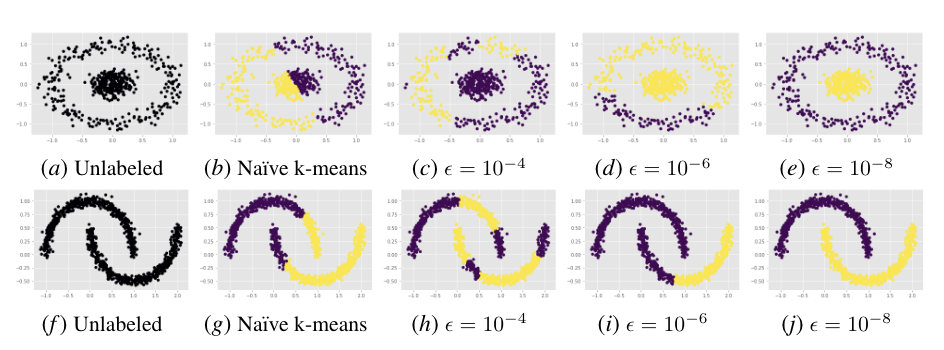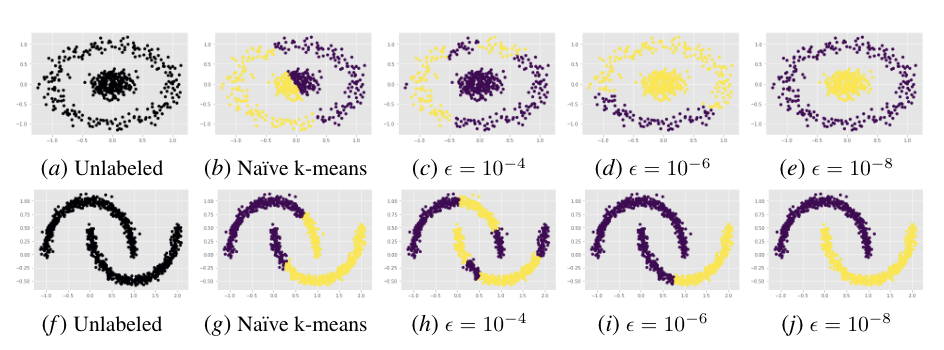
Performance of DMPM on Spectral Clustering. We depict the performance of DMPM ($\rho=\sqrt[3]{\epsilon}$) on dividing a collection of data points into their natural, geometrically-partitioned clusters. The first series (a-e) is the concentric circles dataset while the second series (f-j) is the half-moons dataset. In both series, the first image depicts the unlabeled arrangement, the second depicts a naive application of k-means without spectral clustering, while the last three images depict the performance of k-means assisted by spectral clustering over progressively tighter $\epsilon$ error thresholds (thus, requiring more accurate affinity matrix eigenvector approximations). As $\epsilon$ grows smaller, the data separation improves, eventually achieving perfect classification by $\epsilon=10^{-8}$.